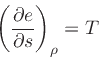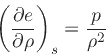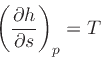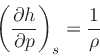



Next: 2.3.2 Definition of often-used
Up: 2.3 A collection of
Previous: 2.3 A collection of
Contents
Index
Differential relations:
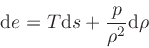 |
(20) |
where  is the internal energy
.
is the internal energy
.
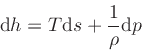 |
(21) |
where the specific enthalpy ,
 , is defined as
, is defined as
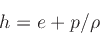 |
(22) |
This implies:
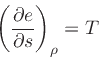 |
(23) |
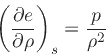 |
(24) |
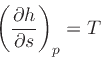 |
(25) |
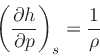 |
(26) |