



The hydrodynamics equations (1) or (2) can be put into the form
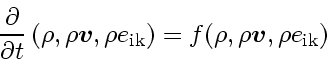 |
(7) |
where the function
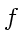 contains the terms with the spatial derivatives.
contains the terms with the spatial derivatives.
Idea:
- take initial state
 given on a grid
given on a grid
- compute
 ,
,  , and
, and 
- compute the spatial derivatives to get the right-hand side of Eq. (7)
- get a small change of

- update

- restart at 2
There 1000 ways how this can go wrong...
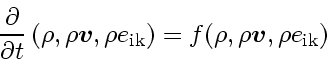
 given on a grid
given on a grid

