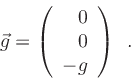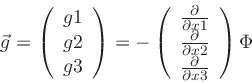



Next: 2.2 Magnetohydrodynamics (W. Schaffenberger)
Up: 2. Equations
Previous: 2. Equations
Contents
Index
The hydrodynamics equations are expressed as conservation relations
plus source terms for
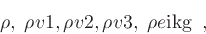 |
(1) |
the mass density,
the three mass fluxes
and the total energy density (per volume), respectively.
Each quantity 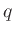 has its corresponding flux
has its corresponding flux 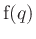 and
possibly source term
and
possibly source term 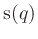 .
For convenience,
.
For convenience,
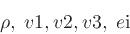 |
(2) |
are chosen as independent quantities.
The conserved quantities are purely algebraic combinations of these.
The 3D hydrodynamics equations,
including source terms due to gravity, are
the mass conservation equation
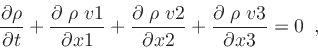 |
(3) |
the momentum equation
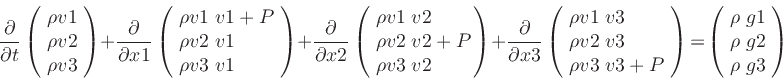 |
(4) |
and the energy equation including radiative heating term 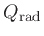
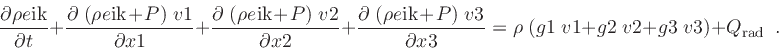 |
(5) |
The pressure 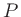 is computed from density
is computed from density 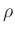 and internal energy
and internal energy 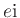 via a (tabulated)
equation of state
via a (tabulated)
equation of state
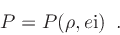 |
(6) |
For local models the gravity field is simply given by
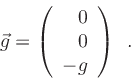 |
(7) |
For global models it is given by
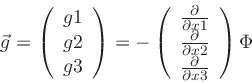 |
(8) |
with
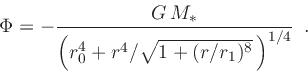 |
(9) |
Here, 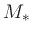 is the mass of the star to be modeled;
is the mass of the star to be modeled;
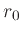 and
and 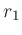 are free smoothing parameters.
In addition, there are equations for the non-local radiation transport.
If grey opacity tables are used, the opacities
are free smoothing parameters.
In addition, there are equations for the non-local radiation transport.
If grey opacity tables are used, the opacities 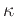 are a simple function
of e.g. temperature
are a simple function
of e.g. temperature 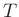 and pressure
and pressure 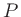
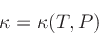 |
(10) |
and the source function 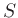 is given by
is given by
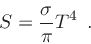 |
(11) |
The change in optical depth 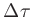 along a path with length
along a path with length 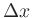 is than
is than
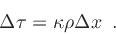 |
(12) |
The variation of the intensity 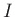 with optical depth
with optical depth 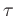 along a ray
with orientation
along a ray
with orientation
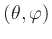 can be described by the simple differential equation
can be described by the simple differential equation
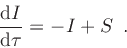 |
(13) |
The radiative energy flux is given by
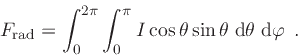 |
(14) |
The energy change can than be computed from the flux divergence with
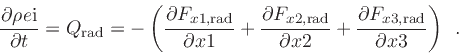 |
(15) |




Next: 2.2 Magnetohydrodynamics (W. Schaffenberger)
Up: 2. Equations
Previous: 2. Equations
Contents
Index