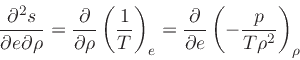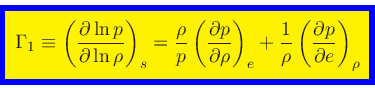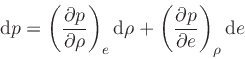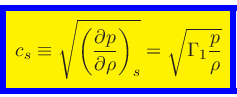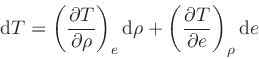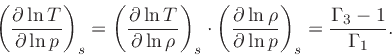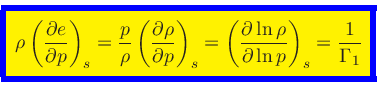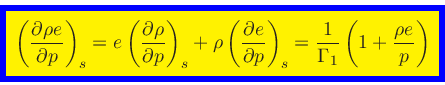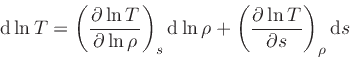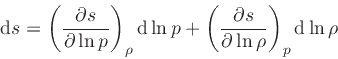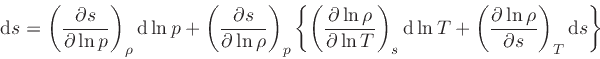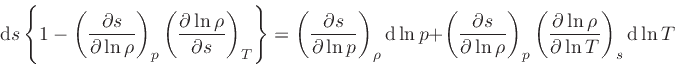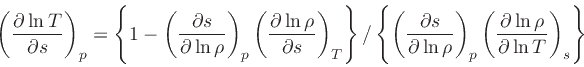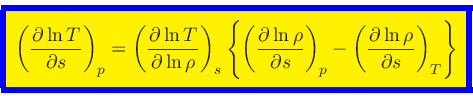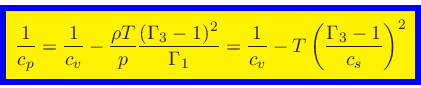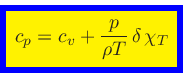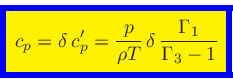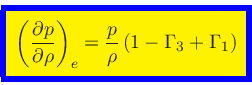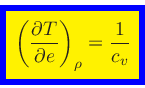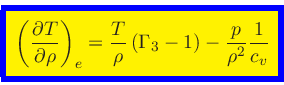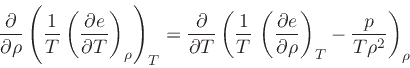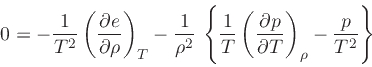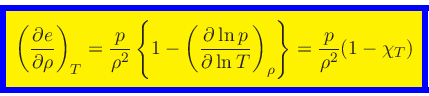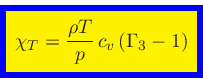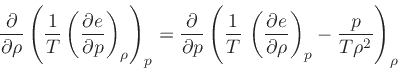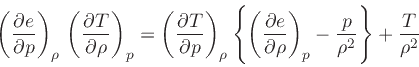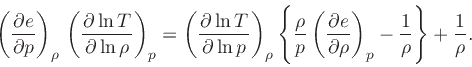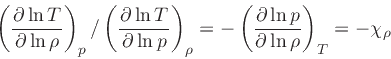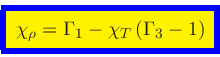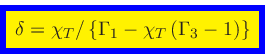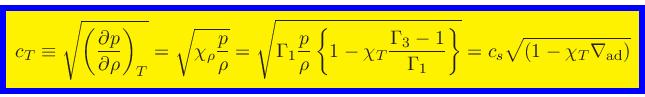



Next: 2.3.5 Ideal gas with
Up: 2.3 A collection of
Previous: 2.3.3 CO5BOLD equation of
Contents
Index
First, the missing derivative
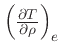 can be found from the relation:
can be found from the relation:
 |
(38) |
which is obtained from the equality of the mixed derivatives in
Eq.(20), written as:
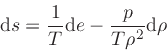 |
(39) |
Then
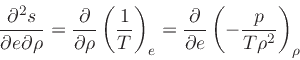 |
(40) |
First adiabatic exponent:
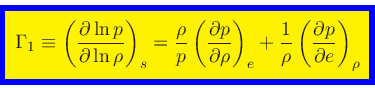 |
(41) |
This relation is obtained by combining Eq.(20) with the identity
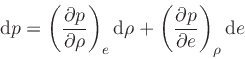 |
(42) |
The adiabatic sound speed
is then obtained as
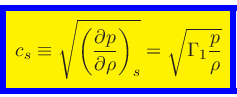 |
(43) |
Third adiabatic exponent:
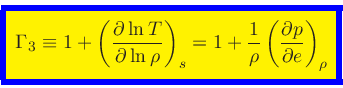 |
(44) |
This relation is obtained by combining Eq.(20) with the identity
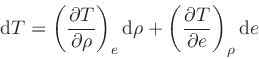 |
(45) |
and then using Eq.(38).
Adiabatic temperature gradient:
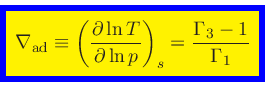 |
(46) |
since
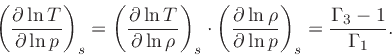 |
(47) |
Adiabatic energy changes:
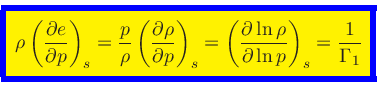 |
(48) |
or
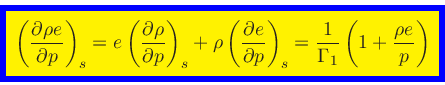 |
(49) |
We define the coefficients  and
and 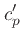 through the
relation
through the
relation
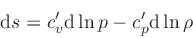 |
(50) |
Entropy change at constant density:
 |
(51) |
This relation is obtained from the equality of the mixed derivatives in
Eq.(20) together with Eq.(44).
Entropy change at constant pressure:
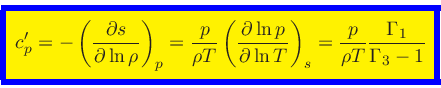 |
(52) |
This relation is obtained from the equality of the mixed derivatives in
Eq.(21) together with Eq.(46).
Specific heat at constant density:
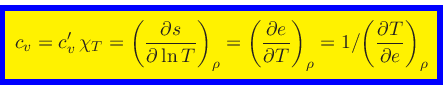 |
(53) |
To derive the specific heat at constant pressure, we start from the relation
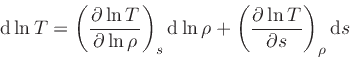 |
(54) |
from which we get
 |
(55) |
Using Eqs.(44) and (53), we obtain
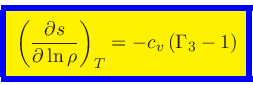 |
(56) |
Now
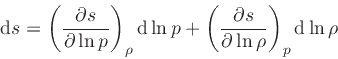 |
(57) |
or
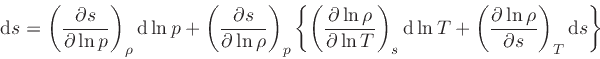 |
(58) |
hence
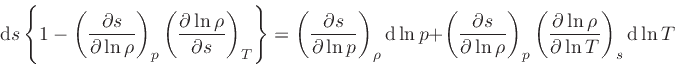 |
(59) |
and finally
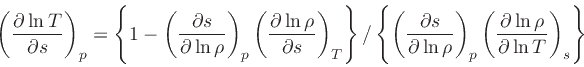 |
(60) |
or
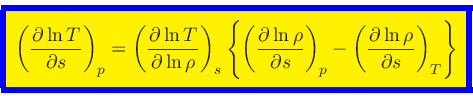 |
(61) |
Using Eqs.(27), (44), (52), (56),
we finally obtain the relation for the specific heat at constant pressure:
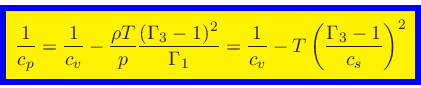 |
(62) |
Alternatively, 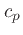 can be obtained from Eq.(32)
can be obtained from Eq.(32)
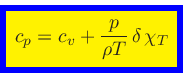 |
(63) |
or from
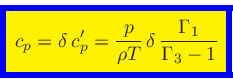 |
(64) |
once 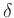 and
and 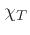 are known (see below).
are known (see below).
We can now express the thermodynamic coefficients provided by CO5BOLD
in terms of 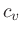 ,
, 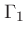 ,
, 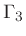 , and
, and
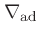 :
:
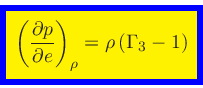 |
(65) |
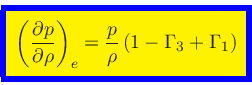 |
(66) |
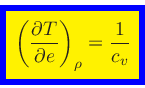 |
(67) |
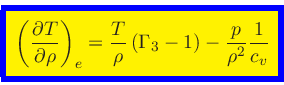 |
(68) |
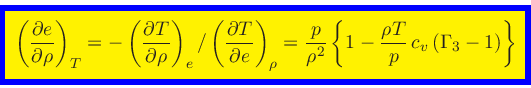 |
(69) |
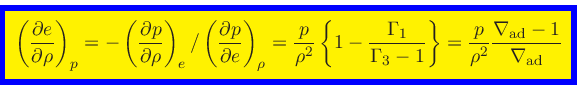 |
(70) |
We consider again Eq.(39), replacing 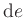 by
by
 |
(71) |
so
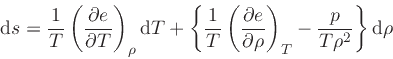 |
(72) |
The requirement that the mixed derivatives must be equal then yields
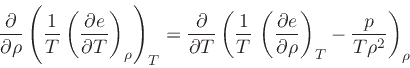 |
(73) |
or
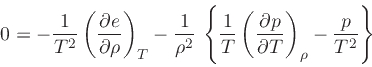 |
(74) |
Finally,
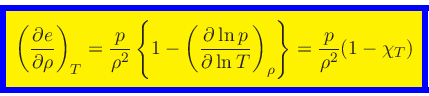 |
(75) |
Comparison with Eq.(69) implies
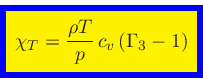 |
(76) |
Similarly, replacing 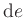 by
by
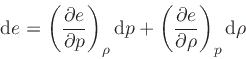 |
(77) |
in Eq.(39), we get
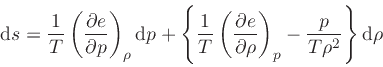 |
(78) |
and the requirement that the mixed derivatives must be equal then yields
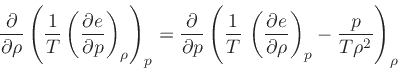 |
(79) |
or
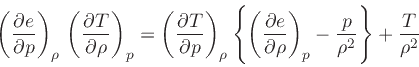 |
(80) |
or
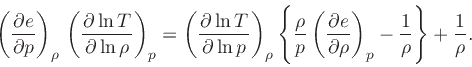 |
(81) |
Since
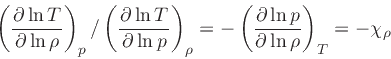 |
(82) |
we finally obtain, using Eqs.(29), (65) and (70),
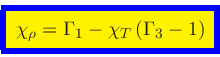 |
(83) |
and
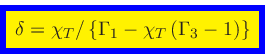 |
(84) |
The isothermal sound speed
is then obtained as
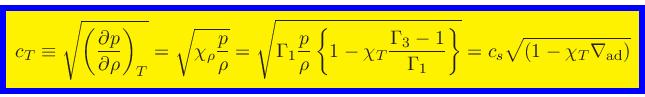 |
(85) |




Next: 2.3.5 Ideal gas with
Up: 2.3 A collection of
Previous: 2.3.3 CO5BOLD equation of
Contents
Index

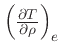 can be found from the relation:
can be found from the relation: