3.1.8 Similarity solutions II

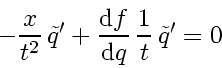
Inserting this ansatz (175) into Eq. (173) gives for $t > 0$

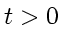
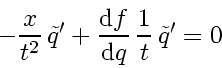$$- \frac{x}{t^2} \tilde{q}' + \frac{\mathrm{d} f}{\mathrm{d} q} \frac{1}{t} \tilde{q}' = 0$$ (176)

with the solutions

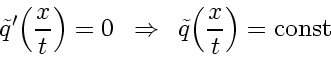$$\tilde{q}' \! \left( \frac{x}{t} \right) = 0 \enspace \Rig... ...nspace \tilde{q} \! \left( \frac{x}{t} \right) = \mbox{const}$$ (177)

or

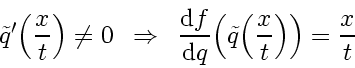$$\tilde{q}' \! \left( \frac{x}{t} \right) \neq 0 \enspace \... ... \tilde{q} \! \left( \frac{x}{t} \right) \right) = \frac{x}{t}$$ (178)

which for Burgers' equation gives

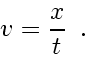$$v_{} = \frac{x}{t} \enspace .$$ (179)

This solution (179) describes the state within a rarefaction fan whereas Eq. (177) applies everywhere else (outside of rarefaction waves and shocks).