



- For most Riemann problems (Fig. 26)
the CIR scheme (185)
actually produces initially the exact result.
- Only for a transonic rarefaction wave
(as in the last example in Fig. 30)
it differs.
-
Godunov's idea:
Solve a Riemann problem
(
 Riemann solver)
at every cell boundary and derive the corresponding flux over the boundary.
Riemann solver)
at every cell boundary and derive the corresponding flux over the boundary.
- For Burgers' equation the flux through the stagnation point (
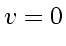 )
in a transonic rarefaction wave is
)
in a transonic rarefaction wave is
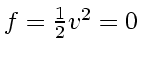 .
.
 Extend the CIR scheme to get a
Godunov-type scheme
by defining
Extend the CIR scheme to get a
Godunov-type scheme
by defining
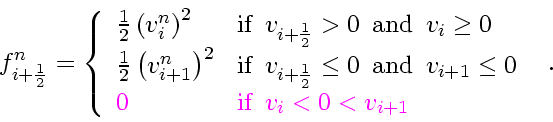 |
(189) |
The additional branch is an
entropy fix
to the CIR scheme.
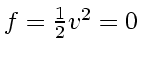 .
.
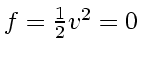 .
.