



Idea:
Perform hydrodynamics simulations in 2D and 3D where
an expanding supernova bubble
(classical Sedov problem)
collides with a slowly moving interstellar molecular cloud
(a region with higher density in pressure-equilibrium
with its environment).
Physical questions behind the experiments:
- What does happen to the cloud after the collision?
- Which velocities are induced?
- Is material mainly compressed so that star formation might become possible?
Concrete: what is the maximum density found within the cloud after the collision?
- Or is the cloud essentially dispersed?
Concrete: How much mass is left?
In detail:
- Installation of CLAWPACK:
- Download the CLAWPACK
package
by Randall J. LeVeque.
- Read the instructions (and - if necessary - look into the book by Randall LeVeque).
- Install the main program package and relevant application packages
(especially the 2D and 3D examples)
on your favorite computer (a FORTRAN77 compiler, e.g.
gnu f77, is needed).
- Perform some of the test simulations coming with the package.
- Produce the output files in ASCII or preferably HDF4 format.
- Read the data with a plotting program (MATLAB is recommended by the author.
IDL can read HDF, too).
- Check out particularly the examples of a plane-parallel shock waves hitting a bubble
in the ``applications-Euler-2D'' and ``-3D'' directories.
- Preliminary 2D experiments:
- Modify the pre-defined setup to account for an expanding blast wave and
a cold (perhaps irregularly shaped) gas cloud:
- Background:
The initial mass density and internal energy is constant everywhere
(and could be adopted from the pre-defined examples).
The grid is equidistant.
The number of grid points should be optimized during tests (50x80 might be a start).
Boundary conditions: constant (zero gradient).
Initial velocities could be set to zero.
However, a better choice is to set all velocities to a constant value,
so that the cloud moves towards the blast wave (to save some grid points).
- Cloud:
The material within the cloud is defined by a 10 times higher density.
A smaller (by the same factor) temperature results in a constant pressure.
The shape of the cloud could be circular (spherical) or even be more
interesting: make a choice.
The high-density cloud in pressure-equilibrium moving with constant velocity
is exactly the linear advection problem!
- Supernova blast wave:
The internal energy at a single grid point (outside the cloud)
could be increased by a significant amount (e.g. by an arbitrary factor 10
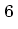 ).
However, stability and efficiency considerations (small time-step) might
require a spreading of this energy over a certain volume (a few grid cells with a
smaller increase in energy).
Such a simplified ``supernova explosion'' is called ``Sedov problem''.
).
However, stability and efficiency considerations (small time-step) might
require a spreading of this energy over a certain volume (a few grid cells with a
smaller increase in energy).
Such a simplified ``supernova explosion'' is called ``Sedov problem''.
- Perform (a few) test runs in 2D.
- Produce output files at about 10 critical time-steps: e.g. some time after the ignition of the supernova,
just before the blast wave hits the cloud,
just after the blast wave hits the cloud,
blast wave has traversed the cloud half way through,
blast wave has passed the cloud.
- A recommended setup for CLAWPACK would be:
Roe-solver,
van Leer slope-limiter,
50x80 grid points,
open (zero gradient) boundary conditions.
- However, the adequateness has to be verified
by comparing variations in initial conditions and setups:
- Is the quality of the solution with a fully non-linear Riemann-solver
worth the additional computational work?
Try a ful Riemann-solver and check if e.g. the sharpness of the
expanding shock or the density profile of the cloud improve.
- Compare runs with some of the slope functions
(Lax-Wendroff, vanLeer, Superbee)
already encountered in the first exercise:
Is the aggressive Superbee scheme the best?
How does the overshooting Lax-Wendroff scheme perform?
Compare again shock and cloud profile and the number of ``features''
after the collision of the blast wave with the cloud.
- How many grid points are necessary?
Is 50x80 OK?
Try a doubling (and another, if possible) and check if the solution
looks qualitatively the same.
Is a doubling in 3D possible with 100x160x160 points?
- Are standard open (zero gradient) boundary conditions appropriate?
Look for artifacts near the boundaries.
- Final 3D experiments:
- Choose the ``best'' parameter set determined by the 2D runs
(slope-limiter, number of grid points, ...).
- Extend the initial conditions to 3D.
- Perform runs with standard and double resolution.
- Compare the results and check the influence of the increased resolution.
Option 1 (3 more points): radiation-transport as post-processing step
- Rays only along main axis (axes).
- First step: Simple ``continuum'' opacities: the result should display
the density and temperature distribution in a ``ray-tracing'' like manner.
- Second step: ``Realistic'' radiation transport: single line (in LTE?),
including Doppler shifts,...
- Compare the resulting maps (and spectra) for the two runs with different resolutions.
Option 2 (alternative to option 1: 3 more points): MPI version
- Install MPICLAW on a parallel computer (zeipel, UPPMAX,...).
- Perform runs with at least one further doubling of the number of grid points.
- Determine the scaling of the performance of the scheme when used on more and more processors.




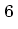 ).
However, stability and efficiency considerations (small time-step) might
require a spreading of this energy over a certain volume (a few grid cells with a
smaller increase in energy).
Such a simplified ``supernova explosion'' is called ``Sedov problem''.
).
However, stability and efficiency considerations (small time-step) might
require a spreading of this energy over a certain volume (a few grid cells with a
smaller increase in energy).
Such a simplified ``supernova explosion'' is called ``Sedov problem''.