



Next: 3 Program Files, Installation,
Up: CO5BOLD User Manual
Previous: 1 Introduction
Contents
Index
The 3D hydrodynamics equations,
including source terms due to gravity, are
the mass conservation equation
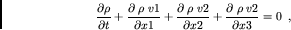 |
(1) |
the momentum equation
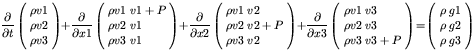 |
(2) |
and the energy equation
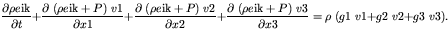 |
(3) |
In addition, there are equations for the 3D tensor viscosity and the non-local radiation transport.