Without source terms the only change between time
![]() and
and
![]() to the amount of a conserved variable inside a volume
to the amount of a conserved variable inside a volume
![]() comes from the flux through its surface
comes from the flux through its surface
![]() .
.
Integrating Eqs. (8) to (10) over that surface and time thus gives
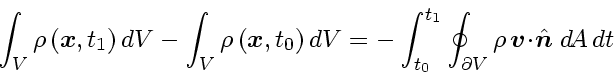 |
(11) |
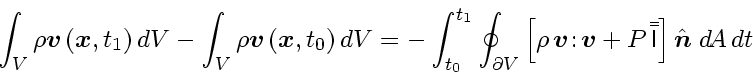 |
(12) |
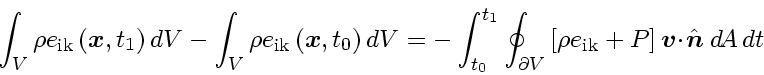 |
(13) |
| (14) |