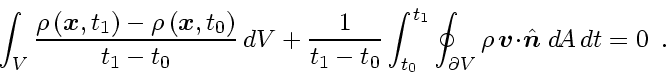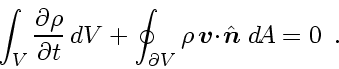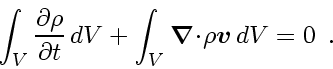



To transform the mass transport equation into differential form
the first line of Eq. (15) is divided by
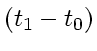 ,
,
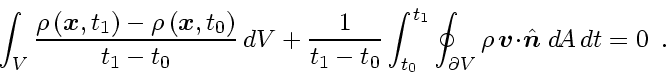 |
(16) |
Taking the limes
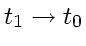 and assuming that the derivative
and assuming that the derivative
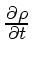 exists
for all
exists
for all
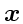 we get
we get
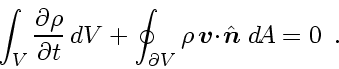 |
(17) |
Now, the
Gauß theorem
is applied (assuming that the divergence
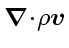 does exist) to
transform the surface integral into a volume integral.
We get
does exist) to
transform the surface integral into a volume integral.
We get
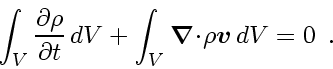 |
(18) |
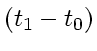 ,
,
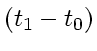 ,
,