



1.5.3 Hyperbolic system
A linear system (43) of PDEs
is called
hyperbolic
if
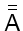 is
diagonalizable,
i.e., there exists a matrix
is
diagonalizable,
i.e., there exists a matrix
 with
with
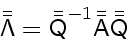 |
(46) |
and
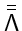 is in diagonal form
(with real numbers on the diagonal: the eigenvalues of
is in diagonal form
(with real numbers on the diagonal: the eigenvalues of
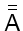 ).
).
With the definition
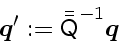 |
(47) |
Eq. (43) gets the
characteristic form
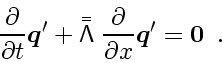 |
(48) |
This is now a set of independent equations, each of the simple form
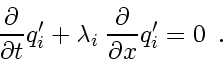 |
(49) |
A quasi-linear system with
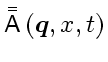 can be hyperbolic at point
can be hyperbolic at point
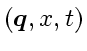 .
.
![]() is
diagonalizable,
i.e., there exists a matrix
is
diagonalizable,
i.e., there exists a matrix
![]() with
with
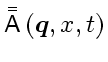 can be hyperbolic at point
can be hyperbolic at point
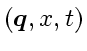 .
.