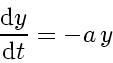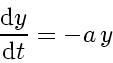



The simple ordinary differential equation (ODE)
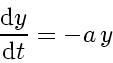 |
(71) |
with initial value
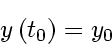 |
(72) |
is of first order and linear with constant coefficient
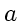 .
It has the obvious solution
.
It has the obvious solution
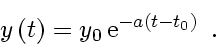 |
(73) |
For discrete time-steps
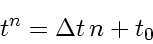 |
(74) |
the straight-forward replacement
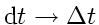 gives the most simple discretization
(explicit Euler scheme: approximation of
gives the most simple discretization
(explicit Euler scheme: approximation of
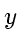 by a piecewise linear curve)
by a piecewise linear curve)
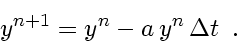 |
(75) |