2.3.15 Consistency - stability - convergence

• Consistency: A numerical scheme is consistent if its discrete operator (with finite differences) converges towards the continuous operator (with derivatives) of the PDE for 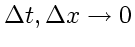$\Delta t, \Delta x\rightarrow 0$ (vanishing truncation error).
• Stability: ``Noise'' (from initial conditions, round-off errors,...) does not grow.
• Convergence: The solution of the numerical scheme converges towards the real solution of the PDE for $\Delta t, \Delta x\rightarrow 0$.

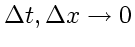Lax's equivalence theorem: ``Given a properly posed initial value problem and a finite-difference approximation to it that satisfies the consistency condition, stability is the necessary and sufficient condition for convergence.''

• Consistency: discrete operator 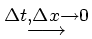$\stackrel{\Delta t, \Delta x\rightarrow 0}{\longrightarrow}$ PDE operator
• Stability: discrete operator does not amplify ``noise''
• Convergence: Numerical solution 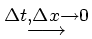$\stackrel{\Delta t, \Delta x\rightarrow 0}{\longrightarrow}$ real solution

Lax's equivalence theorem: consistency 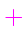$+$ stability $\Leftrightarrow$ convergence