2.3.17 Further concepts

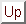
Important properties of a numerical scheme:

• Consistency (otherwise it does not describe the PDE)
• Stability (and therefore convergence of the solution)
• Conservativity (to prevent leakages)

Further desirable properties of a numerical scheme or code:

• Accuracy: high-order convergence in smooth regions (high-order truncation error), good approximation even at finite resolution, minimal artifacts near discontinuities
• Positivity (boundedness): 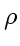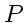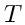$\rho$, $P$, $T$ always positive
• Simplicity: code should be easy to understand, maintain, and extend
• Efficiency: code should be fast (on a variety of machines)

The non-linear system of the hydrodynamic equations will put additional weight on conservativity and positivity.