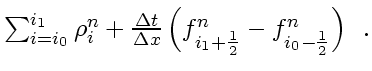



After computing e.g. from the fluxes in the cells
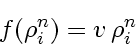 |
(97) |
the fluxes at cell boundaries
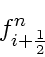 |
(98) |
that characterize a method, the update can be done by the formula
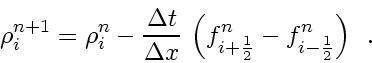 |
(99) |
This is the
conservation form because
the density changes only due to fluxes through the boundaries and is conserved otherwise,
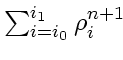
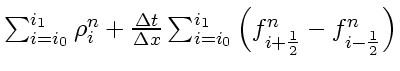
![$\displaystyle \textstyle
\sum_{i=i_0}^{i_1} \rho_i^{n}
+ \frac{\Delta t}{\Delta...
...{i+\frac{1}{2}}^n - f_{i+\frac{1}{2}}^n \right)
- f_{i_0-\frac{1}{2}}^n
\right]$](img223.png)