5.1.1 Operator adding versus splitting

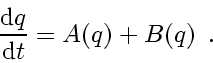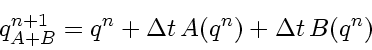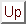
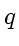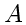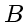Let the time evolution of $\bgroup\color{DEFcolor}$q$\egroup$ be determined by two operators $\bgroup\color{DEFcolor}$A$\egroup$ and $\bgroup\color{DEFcolor}$B$\egroup$ according to

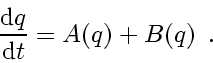$\begin{displaymath} \frac{\mathrm{d} q}{\mathrm{d} t} = A(q) + B(q) \enspace . \end{displaymath}$

(209)

Suppose there are separate numerical schemes available that allow to compute the individual updates

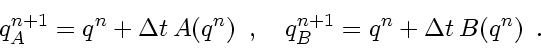$\begin{displaymath} q_A^{n+1} = q^{n} + \Delta t A(q^{n}) \enspace , \enspace \enspace q_B^{n+1} = q^{n} + \Delta t B(q^{n}) \enspace . \end{displaymath}$

(210)

Now, the two schemes could be combined in two ways, e.g. by operator adding

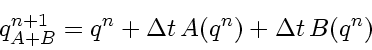$\begin{displaymath} q_{A+B}^{n+1} = q^{n} + \Delta t A(q^{n}) + \Delta t B(q^{n}) \end{displaymath}$

(211)

or Godunov operator splitting

$\displaystyle q_A^{n,*}$	$\textstyle =$	$\displaystyle q^{n} + \Delta t A(q^{n})$
$\displaystyle q_{A+B}^{n+1}$	$\textstyle =$	$\displaystyle q_A^{n,} + \Delta t B(q_A^{n,}) \enspace .$	(212)

The results are generally not the same. Both methods have advantages/drawbacks.