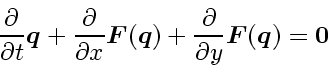 |
(221) |
Directional splitting or dimensional splitting is simply the technique to apply operator splitting to the spatial derivatives in the Euler equations:
becomes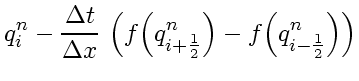 |
|||
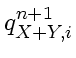 |
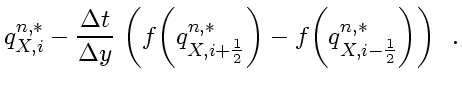 |
(222) |
However, there are cases when a small amount of additional multi-dimensional tensor viscosity is necessary to damp spurious oscillations (even with PPM scheme).