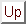
To get accurate results with the Euler scheme (75)
the time-step
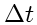has to be very small.
In actual applications one should use a scheme that
- is of
higher order (e.g. a 4th order Runge-Kutta scheme)
to allow much larger time-steps and
to improve the efficiency and accuracy of the scheme
- has a build-in
adjustment of the time-step to guarantee stability
even for variable coefficients
- and/or is
specially adapted for the type of ODE under consideration.
However, the simple scheme in Eq. (75) could - in principle - be used.