


Exercise:
- Solve the 1D linear advection equation (63)
for
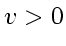 and periodic boundary conditions
with a set of representative schemes:
and periodic boundary conditions
with a set of representative schemes:
- naive FTCS - Eqs. (92) and (105),
- donor cell (FTBS) - Eq. (108),
- Lax-Wendroff - Eq. (111),
- PLM: Minmod - Eq. (135),
- PLM: vanLeer - Eq. (136),
- PLM: Superbee - Eq. (137).
Choose appropriate initial conditions.
- Test and compare the schemes
(for different Courant numbers,
resolutions,
initial conditions).
Check the stability with FFT.
- Write a report containing a few representative plots
and a short evaluation of each scheme.
Detailed questions:
- Naive scheme:
Check that it is unstable.
Could the scheme be used in any way (e.g. for very smooth initial conditions,
small time-steps)?
- The stable schemes:
How many grid points are needed to resolve (and preserve) a structure?
- The stable schemes:
How do diffusion/dispersion depend on Courant number?
- PLM schemes (particularly Superbee):
Do the FFT results hint towards instability?
- Lax-Wendroff scheme:
How much overshoot is acceptable?
What density contrast in the initial condition can be allowed to be sure
that the density remains positive everywhere?