Lambda doubling - calculated TiO lines
-- BertrandPlez 28 Jan 2009:
Some transitions are affected by Lambda-doubling. In that case there are 2 sublevels that give rise to transitions, and if the separation is large enough, they appear in the list as 2 lines with the same parameters except for the parity of the upper and lower level, and a slightly different wavenumber. The degeneracy of these sublevels is 2*J+1. When the Lambda-doubling is too small there are 2 lines with exactly the same data (except the parities). One way to compact the list is to merge these lines and double the gf-value 2*(2*J+1)*f.
For some transitions Lambda-doubling does not exist (if Lambda=0, i.e if one of the states is a Sigma state).
lambda doubling in Plez 2008 calculated lists in gamma prime system
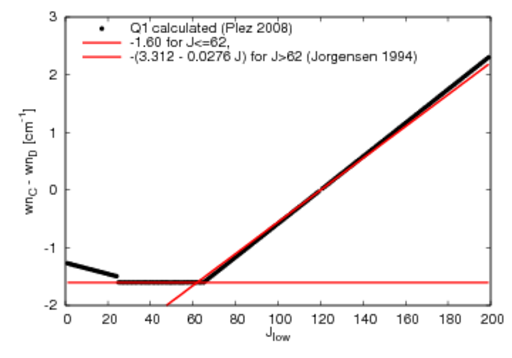
- P1,Q1,R1: lambda doubling resolved for all lines
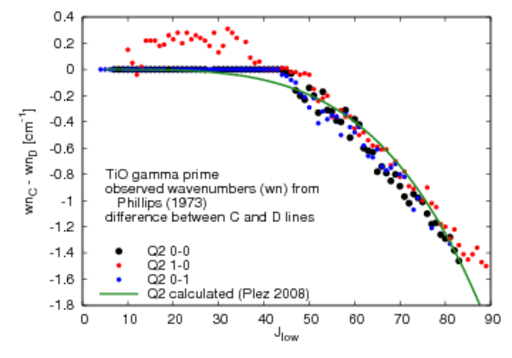
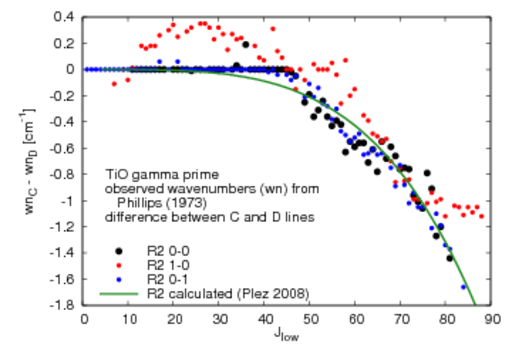
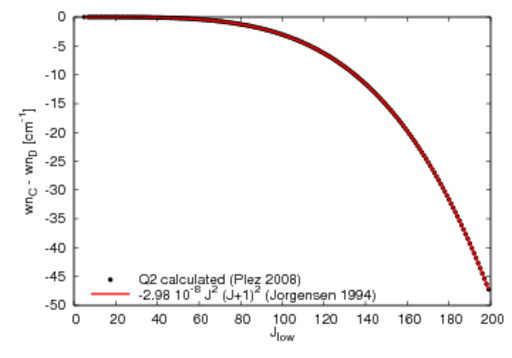
P2,Q2,R2: lambda doubling resolved for Jlow>~10
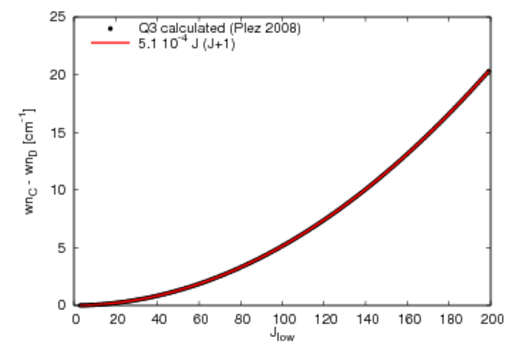
P3,Q3,R3: lambda doubling resolved for Jlow>=3
"resolved" here means: wavenumber difference >=0.001
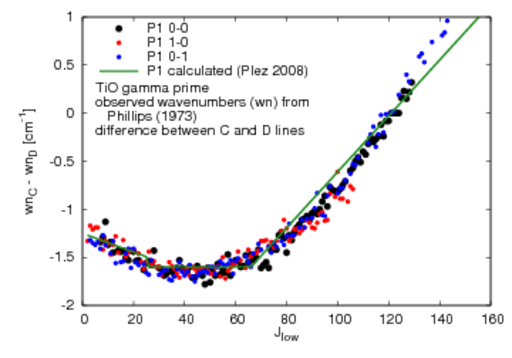
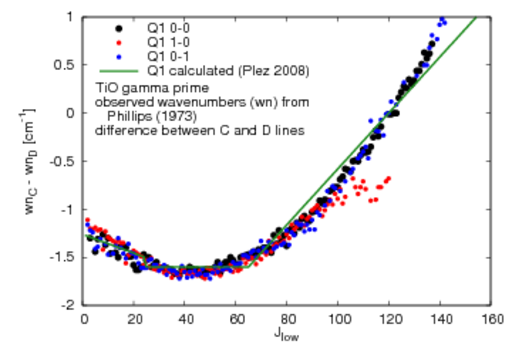
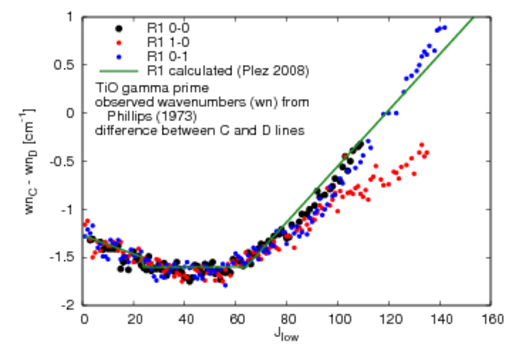
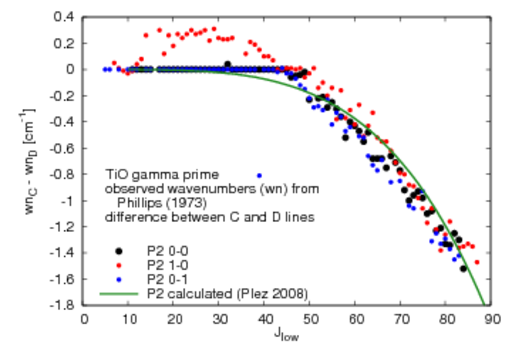
wavenumber (wn) difference for calculated lambda-doubled lines in gamma prime system
- P1,P2,R1,R2 (all v-v):
for even Jlow: wn(syml=-1) > wn(syml=1),
for odd Jlow vice versa
- Q1,Q2: reverse of P
for even Jlow: wn(syml=1) > wn(syml=-1),
for odd Jlow vice versa
- PQR 3: reverse of PQR 1,2
- for the actual values and comparisons to observed wn difference see the plots below (the values are the same for each of the three v-v combinations 0-0, 1-0, 0-1)
- P1,P2,R1,R2 (all v-v):