



Next: 7.1.10 Hydrodynamics control (MHD
Up: 7.1 Parameter file: rhd.par
Previous: 7.1.8 Hydrodynamics control (HD
Contents
Index
Subsections
7.1.9 Hydrodynamics control (HD only)
7.1.9.1 integer n_hydcellsperchunk2
Only for the HD solver and hdsplit=CTU,
the chunk size in 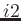 direction can be specified independently.
The default is to used
direction can be specified independently.
The default is to used integer n_hydcellsperchunk.
The approximate number of grid cells per chunk can be specified e.g. with
integer n_hydcellsperchunk2 f=I9 b=4 &
n='Number of cells per hydro chunk 2' &
c0='around 2400 or 1; 0: (default) use n_hydcellsperchunk'
1
The exact number is determined at run time to get (approximately) equal sizes of the individual
chunks.
The choice of this parameter does not affect the result of the computation but
the memory usage and performance, similar to integer n_hydcellsperchunk.
However, as accesses to chunks in 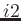 direction span many memory pages,
the access time is longer than for properly aligned chunks in
direction span many memory pages,
the access time is longer than for properly aligned chunks in 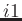 direction
and somewhat larger (twice...) values might be optimal.
Alternatively, a value of
direction
and somewhat larger (twice...) values might be optimal.
Alternatively, a value of n_hydcellsperchunk2=1 causes a two-stage
access where first an entire 2D slice is transposed and copied to achieve
properly alignment and then the normal chunk size (specified with integer n_hydcellsperchunk)
is used in a consecutive step.
7.1.9.2 integer n_hydcellsperchunk3
Only for the HD solver,
the chunk size in 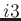 direction can be specified independently.
The default is to used
direction can be specified independently.
The default is to used integer n_hydcellsperchunk.
The approximate number of grid cells per chunk can be specified e.g. with
integer n_hydcellsperchunk3 f=I9 b=4 &
n='Number of cells per hydro chunk 3' &
c0='around 2400 or 1; 0: (default) use n_hydcellsperchunk'
1
The exact number is determined at run time to get (approximately) equal sizes of the individual
chunks.
The choice of this parameter does not affect the result of the computation but
the memory usage and performance, similar to integer n_hydcellsperchunk.
However, as accesses to chunks in 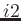 direction span many memory pages,
the access time is longer than for properly aligned chunks in
direction span many memory pages,
the access time is longer than for properly aligned chunks in 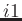 direction
and somewhat larger (twice...) values might be optimal.
Alternatively, a value of
direction
and somewhat larger (twice...) values might be optimal.
Alternatively, a value of n_hydcellsperchunk3=1 causes a two-stage
access where first an entire 2D slice is transposed and copied to achieve
properly alignment and then the normal chunk size (specified with integer n_hydcellsperchunk)
is used in a consecutive step.
7.1.9.3 integer n_hydrkiter
In the case of hdscheme = Roe and hdtimeintegrationscheme = RungeKutta2
(and only there), the default number of Runge-Kutta sub steps
can be increased relative to the default value 2 to improve the performance
in the case of a large ratio of radiative to hydrodynamical time scales.
The parameter can be set e.g. with
integer n_hydrkiter f=I9 b=4 &
n='Number of Runge-Kutta sub steps' &
c0='2: default; 3: some acceleration'
3
Reasonable values are
2: (default) The standard predictor-corrector 2nd-order Runge-Kutta step number.
Cost: 2; advance 1; C_hydSoundCourantMax=1/3 =0.333
3: Typical recommended value.
Cost: 3; advance 2; C_hydSoundCourantMax=1/3*(3/2)^(1/3)=0.381
5: Rather large, still sensible value.
Cost: 5; advance 4; C_hydSoundCourantMax=1/3*(5/4)^(1/3)=0.358
7.1.9.4 real c_hydlowmachcsfactor
For very low Mach numbers
the over-sensitive sound-wave detection of the Roe solver (for 2D and 3D cases)
can be suppressed by choosing a non-zero value for real c_hydlowmachcsfactor.
This is in fact a tiny modification of the Roe solver but changes its behavior
significantly and requires
(for C_hydLowMachcsFactor>0.0)
hdsplit=unsplit and
hdtimeintegrationscheme=RungeKutta2 or hdtimeintegrationscheme=RungeKutta3.
The value can be set e.g. with
real c_hydlowmachcsfactor f=E15.8 b=4 &
n='Low-Mach-Number sound-speed reduction parameter' &
c0='<=0.0: off (old settings, recommended default)' &
c1='1.0: small value; 2.0: reasonable value; 5.0: large value'
2.0
Typical choices are
0.0: The extra reduction factor is not applied.
This is the standard Roe scheme.
It is still the recommended default, excepd for very-low-Mach-number flows.
1.0: Smallest meaningful value to switch on the reduction.
2.0: Reasonable value
5.0: Rather large value
The default is not to use this reduction and leave the parameter at 0.0.
However, the improvement for low-Mach-number flows is significant.
This parameter is not recognized by the MHD module.
7.1.9.5 real c_hydlowmachcsbase
For very low Mach numbers
the over-sensitive sound-wave detection of the Roe solver (for 2D and 3D cases)
can be suppressed by choosing a non-zero value for real c_hydlowmachcsfactor.
With real c_hydlowmachcsbase, a minimum value can be chosen as, e.g., in
real c_hydlowmachcsbase f=E15.8 b=4 &
n='Low-Mach-Number sound-speed reduction base value' &
c0='<=0.0: off (old settings); 0.001-0.02: reasonable values'
0.001
Typical choices are
0.0: The extra reduction factor is not applied.
This is the standard Roe scheme.
It is still the recommended default, excepd for very-low-Mach-number flows.
<1.0E-06: Dangerously small values
1.0E-06: Default
0.001 to 0.02: Reasonable values
1.0: Switch off the low-Mach-number sound-speed reduction
7.1.9.6 real c_hydsmallfluctfactor
In various equations in the Roe solver, an estimate of the relative size
of fluctuations is made.
With real c_hydsmallfluctfactor, a scaling factor can be chosen to
fine tune the regime of the small-fluctation treatment, as, e.g., in
real c_hydsmallfluctfactor f=E15.8 b=4 &
n='Small/large-fluctuation estimate parameter' &
c0='<1.0: smaller relative fluctuations ; 1.0: default; >1.0: larger fluctuations'
1.0
Typical choices are
<1.0: Extend the small-fluctuation treatment towards larger fluctuations.
This can can result in a nicer entropy profile but might be unstable.
1.0: Default
0.5, 1.0, 2.0, 5.0: Reasonable values
>1.0: Extend the large-fluctuation treatment towards smaller fluctuations.
This improves stability but leads to artefacts in the entropy stratification
under near-adiabatic conditions.
7.1.9.7 real c_slopered
A new extra stabilization mechanism can be activated that reduces the slope
and flattens the reconstruction function in case of a strong density contrast
(
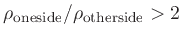 between neighboring cells).
This value can be set e.g. with
between neighboring cells).
This value can be set e.g. with
real c_slopered f=E15.8 b=4 &
n='Slope reduction parameter in case of strong density contrast' u=1 &
c0='0.00: off (default), 0.02: reasonable value, 0.10: large value'
0.02
Typical choices are
0.0: Slope reduction switched off.
Original reconstruction is used.
0.02: Moderate slope reduction in case of large density jumps.
0.10: More pronounced slope reduction in case of strong density contrast.
The default is not to use this trick and leave the parameter at 0.0.
However, if numerical problems occur close to strong density jumps
one can try to cure them by setting it e.g., to 0.02 or so.
One could even think off other criteria (e.g., low temperatures,
very high Mach numbers,...) to activate this slope reduction. That could
be implemented if it would deem beneficial.
This parameter is not recognized by the MHD module.
7.1.9.8 real c_reccontshift
The second-order reconstruction schemes except FRcont have the option to make
the reconstruction even more continuous in the case of very low Mach numbers,
controlled with C_RecContShift and C_RecContSteep.
The value can be set e.g. with
real c_reccontshift f=E15.8 b=4 &
n='Enhanced reconstruction continuation parameter 1 for shifting' &
c0='0.0: off; 1.0: reasonable value'
0.2
Typical choices are
0.0: No attempt is made to make the reconstruction more continuous.
The original reconstruction is used.
0.1: Make the transition to a smoother reconstruction at lower Mach numbers.
1.0: Reasonable value.
10.0: Make the transition to a smoother reconstruction at higher Mach numbers.
While the resulting scheme works for solar simulations,
the parameters are really of benefit only in the case of
brown dwarfs or exoplanets or the deep layers of M dwarfs.
This parameter is not recognized by the MHD module.
7.1.9.9 real c_reccontsteep
The second-order reconstruction schemes except FRcont have the option to make
the reconstruction even more continuous in the case of very low Mach numbers,
controlled with C_RecContShift and C_RecContSteep.
The value can be set e.g. with
real c_reccontsteep f=E15.8 b=4 &
n='Enhanced reconstruction continuation parameter 2 for steepening' &
c0='0.0: off; 0.1: reasonable value'
0.5
Typical choices are
0.0: No attempt is made to make the reconstruction more continuous.
The original reconstruction is used.
0.01: Make the transition to a smoother reconstruction steeper
(at even lower Mach numbers)
0.1: Reasonable value.
1.0: Make the transition to a smoother reconstruction smoother
While the resulting scheme works for solar simulations,
the parameters are really of benefit only in the case of
brown dwarfs or exoplanets or the deep layers of M dwarfs.
This parameter is not recognized by the MHD module.
7.1.9.10 real c_recwenoweightcenter
The WENO-style reconstruction schemes VAweno and HBweno
(but not the ``Frankenstein'' versions like FRweno)
allow to set the basic weights for the stencil of each of the three polynomials.
This possibility is given mainly for development purposes.
Users will likely not change the default values.
The specifiers ``central'' and ``right'' refer to the central and right stencil
for finding the value at the right side of a cell.
The ``central'' stencil includes the left and right neighbor cells.
The ``right'' stencil is shifted on point to the right.
The ``left'' stencil is shifted on point to the left, furthest
away from the (right) cell boundary under consideration.
The value for the central stencil can be set e.g. with
real c_recwenoweightcenter f=E15.8 b=4 &
n='Weight of central polynomial' &
c0='Reasonable values: 0.5..0.8; recommended: 0.6'
0.6
Typical choices are
0.3333333: Give the central polynomial 1/3 of the total weight.
Together with c_recwenoweightright=0.5 (Sect.7.1.9.11),
this attributes equal weights to all three stencils.
0.5: Low, but reasonable value.
0.6: Recommended value. Found by a number of empirical tests to be a good choice
together with c_recwenoweightright=0.6666666 (Sect.7.1.9.11).
1.0: Give all weight to the central polynomial.
This essentially kills the central idea of the WENO scheme and only
makes sense for test purposes.
7.1.9.11 real c_recwenoweightright
The WENO-style reconstruction schemes VAweno and HBweno
(but not the ``Frankenstein'' versions like FRweno)
allow to set the basic weights for the stencil of each of the three polynomials.
The value for the ``right'' stencil can be set e.g. with
real c_recwenoweightright f=E15.8 b=4 &
n='Weight of right polynomial' &
c0='Reasonable values: 0.5..0.8; recommended: 0.6666666'
0.6666666
Typical choices are
0.0: Give all weight (that does not go to the central polynomial) to the left polynomial.
For test purposes.
0.5: Give left and right polynomial equal weight.
0.6666666: Recommended value. Found by a number of empirical tests to be a good choice
together with c_recwenoweightcenter=0.6 (Sect.7.1.9.10).
1.0: Give all weight (that does not go to the central polynomial) to the right polynomial.
For test purposes.
7.1.9.12 real c_recwenopsifactor
This parameter represents a factor to the
``Pairwise Smoothness Indicator'' controlling the ``handbrake''
that further stabilizes HBweno
compared to the standard ``Vanilla'' WENO scheme VAweno.
The value of the parameter can be set e.g. with
real c_recwenopsifactor f=E15.8 b=4 &
n='Smoothing factor in case of bad pairwise smoothness match' &
c0='Reasonable values: 0.0..30.0; works only with HBweno'
10.0
Typical choices are
0.0: No additional smoothing.
This reduces HBweno to the (faster) VAweno.
For test purposes only.
1.0: Weak smoothing
4.0: Reasonable value.
16.0: Strong smoothing.
Those values might have to be increased if
c_reccontshift (Sect.7.1.9.8)
is used. Typically,
c_recwenopsifactor 
c_recwenopsifactor/c_reccontshift.
7.1.9.13 character hdtransvelomode
This parameter controls the treatment of advection of transverse velocities.
It can be set e.g. with:
character hdtransvelomode f=A80 b=80 &
n='Mode for transverse velocity advection' &
c0='Normal(default)/CA1/CA2/CA3/CA4(recommended)'
CA4
The choices are
Normal, ' ': Compute flux of transversal momentum with standard Roe treatment
(old, default)
CA1: Compute flux of transversal momentum with consistent advection, version 1.
Use mass flux and upwind density to determine flow speed.
Actually recompute transversal velocities.
CA2: Compute flux of transversal momentum with consistent advection, version 2.
Use mass flux and Roe-mean density (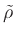 ) to determine flow speed.
Actually recompute transversal velocities.
) to determine flow speed.
Actually recompute transversal velocities.
CA3: Compute flux of transversal momentum with consistent advection, version 3.
Use mass flux and upwind density to determine flow speed.
Compute transversal momentum fluxes from mass flux and diffusive momentum flux.
CA4: Compute flux of transversal momentum with consistent advection, version 4.
Use mass flux and Roe-mean density (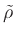 ) to determine flow speed.
Compute transversal momentum fluxes from mass flux and diffusive momentum flux
(recommended).
) to determine flow speed.
Compute transversal momentum fluxes from mass flux and diffusive momentum flux
(recommended).
For instance for a 2D Sedov blast wave problem, the new modes
give less artifacts close to the axes than the old mode Normal.
The four new advection types are made of to choices for the way to compute
the effective flow speed across a cell boundary (different density values
can be used) and two ways to compose the final transversal momentum fluxes.
Version CA4 is recommeded.
This parameter is not recognized by the MHD module.
7.1.9.14 character hdentropywavemode
This parameter controls the computation of the Roe correction flux for the entropy wave.
It can be set e.g. with:
character hdentropywavemode f=A80 b=80 &
n='Mode for entropy wave type' &
c0='Normal/Entropy1/Entropy2/Entropy3M/Entropy3Ms/Entropy3gMps(recommended)'
Entropy3gMps
The choices are
Normal, ' ': Compute entropy-wave flux with standard Roe treatment
from pressure and density,
(old, default).
Entropy1: Compute entropy-wave flux from entropy.
This only works well for small Mach numbers.
Entropy2: Compute entropy-wave flux from entropy and pressure.
Entropy3M: Compute entropy-wave flux from entropy, pressure, and density.
In fact, an cases Normal and Entropy1 are interpolated according to
the Mach number.
Entropy3Ms: Compute entropy-wave flux from entropy, pressure, and density.
In fact, an cases Normal and Entropy1 are interpolated according to
the Mach number and entropy fluctuations.
Entropy3gMps: Compute entropy-wave flux from entropy, pressure, and density.
In fact, an cases Normal and Entropy1 are interpolated according to
the Mach number and fluctuations in pressure (directly and after subtracting
the hydrostatic pressure correction) and entropy. This case is recommended.
The Normal computation with the standard Roe procedure is optimized for shocks
and works also for small fluctuations in density and pressure.
However, in the case of a nearly adiabatic stratification, the density and pressure
fluctuations between adjacent depth points induce some spurious fluxes.
These are avoided by reconstructing the entropy directly (Entropy1).
However, that does not work well for shocks.
Therefore, an interpolation between the standard reconstruction based on
pressure and density and another one based on entropy is recommended
(Entropy3gMps).
This parameter is not recognized by the MHD module.
7.1.9.15 character hdenthalpyavgmode
This parameter controls the type of averaging used to get from the cell-centered
enthalphy (flux) the boundary-centered enthalphy (flux).
To this flux, the Roe corrections are added.
It can be set e.g. with:
character hdenthalpyavgmode f=A80 b=80 &
n='Mode for enthalpy averaging' &
c0='Normal(old default)/CA1/CA1g/CA1gMps(recommeded)/CA1M/CA1Ms/CA1p/CA1s' &
c1='CA2/CA2g/CA2M/CA2p/CA2s/CA3/CA4'
CA1gMps
The choices are
Normal, ' ': Use the standard Roe-averaging of the
enthalpy + kinetic-energy fluxes,
(old, default).
CA1: Average the enthalpy and multiply with the average mass flux.
Average the kinetic energy fluxes as in the standard Roe case.
CA1g: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small fluctuations.
Switch smoothly to the Normal Roe averaging for large non-hydrostatic
pressure fluctuations.
CA1gMps: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small Mach numbers.
Switch smoothly to the Normal Roe averaging
for large Mach numbers or large fluctuations
fluctuations in pressure (directly and after subtracting
the hydrostatic pressure correction) and entropy.
This case is recommended.
CA1M: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small Mach numbers.
Switch smoothly to the Normal Roe averaging for
large Mach numbers.
CA1Ms: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small Mach numbers.
Switch smoothly to the Normal Roe averaging
for large Mach numbers or large entropy fluctuations.
CA1p: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small pressure fluctuations.
Switch smoothly to the Normal Roe averaging for large pressure fluctuations.
CA1s: Use the consistent-advection centering for the average enthalpy flux
as in CA1 for small entropy fluctuations.
Switch smoothly to the Normal Roe averaging for large entropy fluctuations.
CA2: Average the enthalpy plus kinetic energy and multiply with the average mass flux.
CA2g: Use the consistent-advection centering for the average enthalpy plus
kinetic energy flux as in CA2 for small fluctuations.
Switch smoothly to the Normal Roe averaging for large non-hydrostatic
pressure fluctuations.
CA2M: Use the consistent-advection centering for the average enthalpy plus
kinetic energy flux as in CA2 for Mach numbers.
Switch smoothly to the Normal Roe averaging for large Mach numbers.
CA2p: Use the consistent-advection centering for the average enthalpy plus
kinetic energy flux as in CA2 for small pressure fluctuations.
Switch smoothly to the Normal Roe averaging for large pressure fluctuations.
CA2s: Use the consistent-advection centering for the average enthalpy plus
kinetic energy flux as in CA2 for small entropy fluctuations.
Switch smoothly to the Normal Roe averaging for large entropy fluctuations.
CA3: Take the Roe tilde average enthalpy plus kinetic energy and multiply
with the computed mass flux.
This is a more experimental version and not generally recommended.
CA4: Averaging the enthalpy and multiply
with the computed mass flux.
This is a more experimental version and not generally recommended.
Here, 'CA1' and 'CA2' behave in a similar way, whereas'CA3' and 'CA4'
are essentially just for tests.
I prefer the CA1 variant for the time being.
However, both CA1 and CA2 work only well for small fluctuations and Mach numbers.
Therefore, one of the modified schemes should be used.
Again, they are rather similar even if the implemented creteria are rather different.
While most of the versions work for ``ordinary'' main-sequence models,
the comparably pooly resolved red-supergiant models (with large entropy step and Mach numbers)
require a combination of the criteria above.
Therefore, CA1gMps is recommended (for all type of models in general).
This parameter is not recognized by the MHD module.
7.1.9.16 real c_hydpredfactor
The "hydrostatic pressure correction" terms in the two acoustic waves are
always present.
However, for the entropy wave and the "ionization wave" it is not quite clear
if the terms should be there (the classical default) or if they should be
set to zero.
The value of a factor in front of these terms can be set e.g. with
real c_hydpredfactor f=E15.8 b=4 &
n='hydrostatic pressure reduction in waves 3 and 6' u=1 &
c0='0.0: Deactivation of pressure reduction terms' &
c1='1.0: Activation of pressure reduction terms (default)'
0.0
Possible choices are
0.0: Deactivation of pressure reduction terms
in waves 3 and "6" in Roe solver
1.0: Activation of pressure reduction terms
in waves 3 and "6" in Roe solver (default)
This parameter is only recognized for hdEntropyWaveMode='Normal' which
is not recommended, anymore.
This parameter is not recognized by the MHD module.
7.1.9.17 real c_hydsdiffvelo
With this parameter an extra energy diffusion down an entropy step
(after reconstructing the entropy) can be activated.
For the diffusion velocity all three velocity components are used, i.e.,
there is a diffusion even transversal to the flow speed.
This makes the diffusion more isotropic and lets numerical solutions
to the Sedov-blast-wave problem look smoother.
The value can be set e.g. with
real c_hydsdiffvelo f=E15.8 b=4 &
n='Parameter for energy diffusion down an entropy step' u=1 &
c0='typically 1.0'
1.0
Possible choices are for example
0.0: No extra energy diffusion down an entropy gradient (default).
0.2: Small value
1.0: Reasonable value
3.0: Large value
It acts on the entropy but only on the fraction of the jump that is
still there after the reconstruction -
unlike C_hydTdiffLin and C_hydTdiffMach that
act on local temperature minima (see below).
This parameter is not recognized by the MHD module.
7.1.9.18 real c_hydvdiffvelo
With this parameter an extra diffusion of the transversal velocities
(after reconstructing them) can be activated.
For the diffusion velocity all three velocity components are used, i.e.,
there is a diffusion even transversal to the flow speed.
This makes the diffusion more isotropic and lets numerical solutions
to the Sedov-blast-wave problem look smoother.
The value can be set e.g. with
real c_hydvdiffvelo f=E15.8 b=4 &
n='Parameter for transversal momentum diffusion down a velocity step' u=1 &
c0='typically 1.0'
1.0
Possible choices are for example
0.0: No extra energy diffusion down an entropy gradient (default).
0.2: Small value
0.5: Reasonable value
1.0: Reasonable value
3.0: Large value
The type of dissipation that can be added with this option is similar to
that provided by the tensor viscosity (Sect.7.1.11).
Therefore, I recommend to use only small values (0.5 to 1.0)
to reduce the directional dependence of the dissipation applied by the Roe solver
and to use an explicite tensor viscosity (Sect.7.1.11)
in case of emergencies.
This parameter is not recognized by the MHD module (but in fact, the HLLE solver
applies a somewhat similar - but stronger - dissipation by construction).
7.1.9.19 real c_hydtdifflin
The Roe-solver correction does not have any dissipation for standing waves
and very little for slowly moving ones - unlike the MHD-HLLE solver that always
has quite some minimum dissipation (depending on the reconstruction, though).
The small amount of dissipation is a positive feature when it comes e.g.,
to convection with smaller Mach numbers in the deeper layers of a solar model,
or (the absence) of vertical net mass fluxes in a hydrostatic atmosphere.
However, it can be a drawback, e.g., in the case of a transsonic rarefaction wave,
where an entropy fix is applied
(since the beginning, see Leveque ``Numerical Methods for Conservation Laws''),
or in the (rather quiet) center of a Sedov blast wave where a cross-like structure with
comparably low temperature is visible. This artefact can be
removed by applying the standard tensor viscosity including the
energy dissipation down an entropy gradient (controlled with C_visPrturb)
of by the new, rather simple option to the Roe solver
to apply additional energy dissipation down a temperature gradient but only
in cells adjacent to a local temperature minimum (in 1D). It works
nicely for the Sedov blast wave and does not have any visible adverse impact
in any other cases, so far. I don't expect it to do any harm for
convection simulations and recommend to activate it per default.
Cautious people might not like it and see how well it works without,
though. Still, unlike the tensor viscosity with turbulent Prandtl number
there is no viscous flux down the subphotospheric temperature or
entropy gradient (unless there is a local minimum at the bottom).
The linear diffusion can be set e.g. with
real c_hydtdifflin f=E15.8 b=4 &
n='Parameter 1 for energy diffusion near local temperature minimum' u=1 &
c0='typically 0.2, if activated; usually 0.0'
0.0
It just acts on the temperature gradient (in the neighborhood of a local minimum),
whereas C_hydTdiffMach (see below) has an additional factor,
that takes velocity gradients into account,
which prevent this type of diffusion from acting in deeper convective layers.
I recommend as a default C_hydTdiffLin=0.0 and non-zero values only in case
of an emergency and C_hydTdiffMach=1.0 or 2.0 as a default.
These parameters are not recognized by the MHD module.
7.1.9.20 real c_hydtdiffmach
Analogously to c_hydtdifflin,
an additional energy dissipation down a temperature gradient but only
in cells adjacent to a local temperature minimum (in 1D) can be applied,
that has a scaling factor derived from the Mach number.
This Mach-number-dependent diffusion can be set e.g. with
real c_hydtdiffmach f=E15.8 b=4 &
n='Parameter 1 for energy diffusion near local temperature minimum' u=1 &
c0='typically 0.2, if activated; usually 0.0'
1.0
I recommend as a default C_hydTdiffLin=0.0 and non-zero values only in case
of an emergency and C_hydTdiffMach=1.0 or 2.0 as a default.
These parameters are not recognized by the MHD module.




Next: 7.1.10 Hydrodynamics control (MHD
Up: 7.1 Parameter file: rhd.par
Previous: 7.1.8 Hydrodynamics control (HD
Contents
Index