




Next: 3 Program Files, Installation,
Up: 2.2 A collection of
Previous: 2.2.4 Derived thermodynamic coefficients
Contents
Index
2.2.5 Ideal gas with constant specific heats
(polytropic gas)
In this case, we obtain much simpler relations:
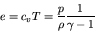 |
(70) |
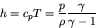 |
(71) |
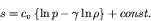 |
(72) |
 |
(73) |
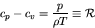 |
(74) |
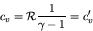 |
(75) |
 |
(76) |
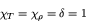 |
(77) |
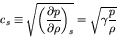 |
(78) |
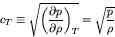 |
(79) |





Next: 3 Program Files, Installation,
Up: 2.2 A collection of
Previous: 2.2.4 Derived thermodynamic coefficients
Contents
Index