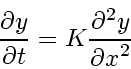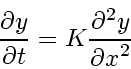



The
heat equation
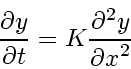 |
(78) |
is a simple
parabolic PDE.
With the initial values
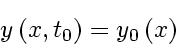 |
(79) |
and boundary values
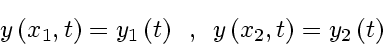 |
(80) |
it models e.g. heat flux or
radiative energy transport in the (optically thick) stellar interior.
In the following examples the conductivity
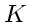 is a constant.
is a constant.