2.5.7 Linear stability analysis: use

Linear stability analysis tells about stability - of linear schemes for linear equations.

Linear stability $\Rightarrow$ convergence for consistent schemes (Sect. 2.3.15).

Ansatz: for

$$\rho_i^n = e^{- ji k \Delta x}$$ (135)

with $k \le k_0=\frac{\pi}{\Delta x}$ we search $A \in \mathbb{C}$ with

$$\rho_i^{n+1} = A \rho_i^n = A e^{- ji k \Delta x} \enspace .$$ (136)

Amount 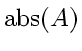$\mbox{abs} \! \left( A \right)$ of $A$ $\Rightarrow$ damping (diffusion) or growth (instability) of waves.

Phase of $A$ $\Rightarrow$ wave speed and dispersion.

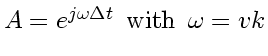Ideally $A = e^{ j\omega \Delta t} \enspace \mbox{with} \enspace \omega = v_{} k$.