
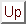



Applying ansatz (135) to the donor cell scheme Eq. (108)
gives, using Eq. (138),
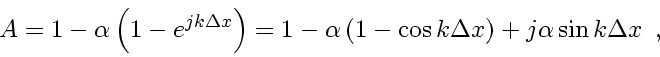 |
(142) |
![\begin{displaymath}
\mbox{abs} \! \left( A \right)
=
[ 1
-
2
\underbrace{\...
...- \cos k \Delta x\right)}_{\ge 0}
]^{\frac{1}{2}}
\enspace ,
\end{displaymath}](img321.png) |
(143) |
![\begin{displaymath}
{\color{HIGH1color}
\mbox{abs} \! \left( A \right)
\le
1...
...\mbox{for} \enspace \alpha \in \left[ 0, 1 \right]
\enspace .
\end{displaymath}](img322.png) |
(144) |
The donor cell scheme is
stable
if the
CFL condition
is fulfilled,
![\begin{displaymath}
{\color{HIGH2color}
\frac{\Delta t}{\Delta x} v_{} \in \left[ 0, 1 \right]
}
\enspace .
\end{displaymath}](img323.png) |
(145) |
Note:
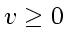 is required (for
is required (for
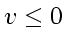 use FTFS).
use FTFS).
Note:
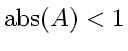 is possible:
numerical viscosity
is possible:
numerical viscosity
Note:
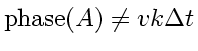 :
dispersion
:
dispersion
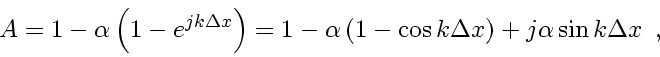
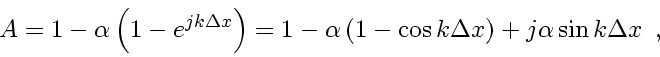
![\begin{displaymath}
\mbox{abs} \! \left( A \right)
=
[ 1
-
2
\underbrace{\...
...- \cos k \Delta x\right)}_{\ge 0}
]^{\frac{1}{2}}
\enspace ,
\end{displaymath}](img321.png)
![\begin{displaymath}
{\color{HIGH2color}
\frac{\Delta t}{\Delta x} v_{} \in \left[ 0, 1 \right]
}
\enspace .
\end{displaymath}](img323.png)