



3.1.1 Viscous and inviscid Burgers' equation
Viscous Burgers' equation:
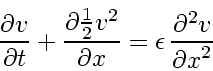 |
(158) |
inviscid
Burgers' equation in
conservation form
(with flux
 )
)
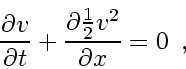 |
(159) |
quasi-linear form
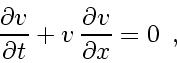 |
(160) |
and integral form
![\begin{displaymath}
\int_{x_0}^{x_1}
\left[ v_{} \! \left( x , t_1 \right)
-
...
...frac{1}{2} v_{}^2 \! \left( x_0 , t \right)
\right]
dt
=
0
\end{displaymath}](img366.png) |
(161) |
- It resembles the linear advection equation (63).
- However, it is
non-linear
with
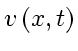 instead of
instead of
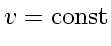 .
.
- It describes the transport of
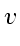 with velocity
with velocity 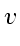 .
.
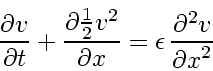
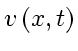 instead of
instead of