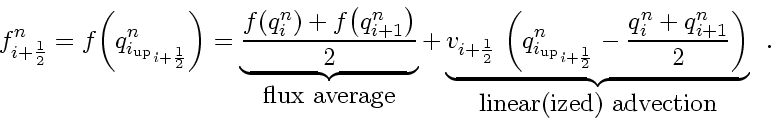3.2.12 Second-order extension of flux formula

Resolving Eq. (192) for the upwind flux that we need as flux (184) for the CIR scheme gives

$$f_{i+\frac{1}{2}}^n = f \! \left( q_{{ i_{\rm up}}_{i+\fr... ...}^n}{2} \right) }_{\mbox{linear(ized) advection}} \enspace .$$ (194)

Remember: This is exactly the simple upwind (CIR) flux.

However, the second term looks like linear advection and suggests to apply a higher-order (eg. slope-limiter) scheme to the localized advection problem for

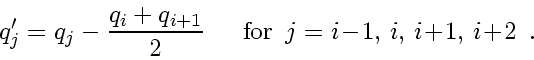$$q'_j = q_j - \frac{q_i + q_{i+1}}{2} \enspace \enspace \en... ...\! - \! 1, i, i \! + \! 1, i \! + \! 2 \enspace .$$ (195)