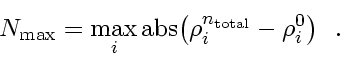



Exercise:
- Solve the 1D linear advection equation (63)
for
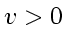 and periodic boundary conditions
in the interval
and periodic boundary conditions
in the interval ![$[-0.5, 0.5]$](img528.png) with a set of representative schemes:
with a set of representative schemes:
- naive FTCS - Eqs. (92) and (110),
- donor cell (FTBS) - Eq. (113),
- Lax-Wendroff - Eq. (116),
- Fromm - Eq. (118),
- PLM: Minmod - Eq. (155),
- PLM: vanLeer - Eq. (156),
- PLM: Superbee - Eq. (157).
- Test and compare the schemes (see below).
- Write a report containing a few representative plots
and a short evaluation of each scheme.
Detailed questions:
- Naive scheme:
Check that it is unstable for non-trivial initial conditions if you
wait long enough.
Nevertheless, could the scheme be used in any way (e.g. for very smooth initial conditions,
small time-steps)?
Try to find a way by experimenting and/or by examining Eq. (140).
- The stable schemes:
Use a Gaussian (
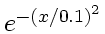 )
and a rectangle (
)
and a rectangle (
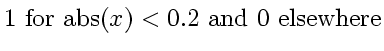 )
as initial conditions.
Choose a reasonable Courant number and keep it fixed.
Simulate a complete revolution (
)
as initial conditions.
Choose a reasonable Courant number and keep it fixed.
Simulate a complete revolution (
 )
to facilitate the comparison with the exact final result (= initial condition).
)
to facilitate the comparison with the exact final result (= initial condition).
- Compare the results for different resolutions
(e.g. 25, 50, 100, 200 grid points).
- Measure the error with the 1-norm
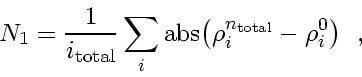 |
(223) |
the Euclidian 2-norm
![\begin{displaymath}
N_2 = \frac{1}{i_{\rm total}} \left[ \sum_i \mbox{abs} \! \...
...{n_{\rm total}} - \rho_i^0 \right)^2 \right]^{1/2}
\enspace ,
\end{displaymath}](img533.png) |
(224) |
and the maximum-norm
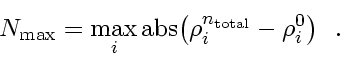 |
(225) |
- How do the errors decrease with resolution (for the different schemes and initial conditions)?
- How many grid points are needed to preserve a structure
(e.g. to push the N2 error below a certain limit)?
- Lax-Wendroff and Fromm scheme:
How much overshoot is acceptable?
What density contrast in the initial condition can be allowed to be sure
that the density remains positive everywhere?
- Perform a numerical FFT analysis
(for the lowest resolution and the Gaussian initial condition only).
Do the FFT results hint towards instability for the non-linear PLM schemes (particularly Superbee)?




![$[-0.5, 0.5]$](img528.png) with a set of representative schemes:
with a set of representative schemes:
![$[-0.5, 0.5]$](img528.png) with a set of representative schemes:
with a set of representative schemes:
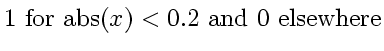 )
as initial conditions.
Choose a reasonable Courant number and keep it fixed.
Simulate a complete revolution (
)
as initial conditions.
Choose a reasonable Courant number and keep it fixed.
Simulate a complete revolution (
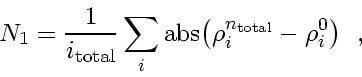
![\begin{displaymath}
N_2 = \frac{1}{i_{\rm total}} \left[ \sum_i \mbox{abs} \! \...
...{n_{\rm total}} - \rho_i^0 \right)^2 \right]^{1/2}
\enspace ,
\end{displaymath}](img533.png)